Bellman Ford Algorithm

It is similar to Dijkstra's algorithm but it can work with graphs in which edges can have negative weights.

Why would one ever have edges with negative weights in real life?

Negative weight edges might seem useless at first but they can explain a lot of phenomena like cashflow, the heat released/absorbed in a chemical reaction, etc.

For instance, if there are different ways to reach from one chemical A to another chemical B, each method will have sub-reactions involving both heat dissipation and absorption.

If we want to find the set of reactions where minimum energy is required, then we will need to be able to factor in the heat absorption as negative weights and heat dissipation as positive weights.

Why do we need to be careful with negative weights?

Negative weight edges can create negative weight cycles i.e. a cycle that will reduce the total path distance by coming back to the same point.

negative weight cycles can give an incorrect result when trying to find out the shortest path — Negative weight cycles can give an incorrect result when trying to find out the shortest path

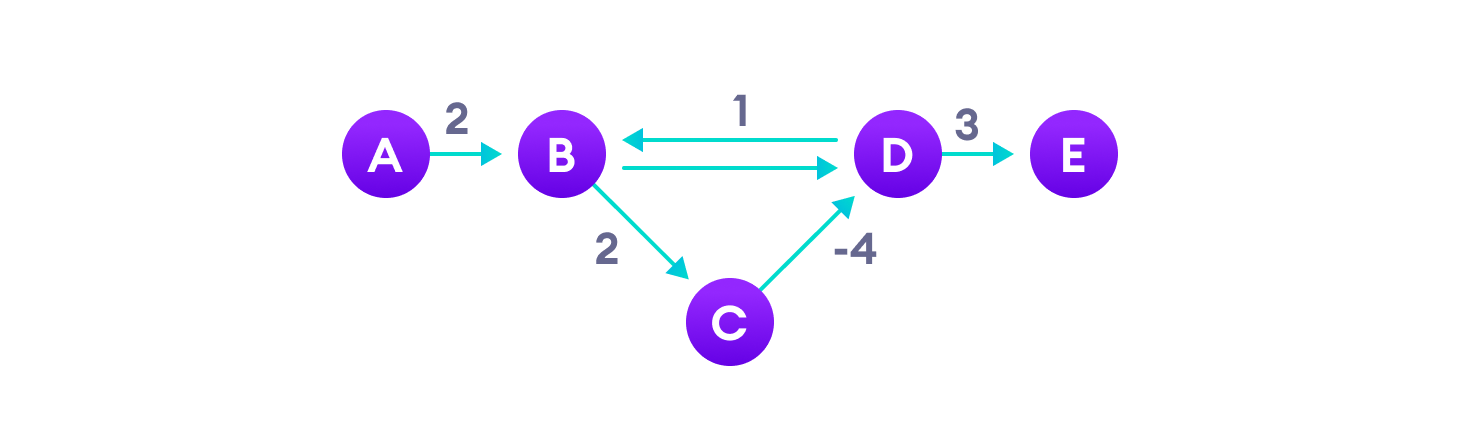
Shortest path algorithms like Dijkstra's Algorithm that aren't able to detect such a cycle can give an incorrect result because they can go through a negative weight cycle and reduce the path length.

How Bellman Ford's algorithm works

Bellman Ford algorithm works by overestimating the length of the path from the starting vertex to all other vertices. Then it iteratively relaxes those estimates by finding new paths that are shorter than the previously overestimated paths.

By doing this repeatedly for all vertices, we can guarantee that the result is optimized.

steps for bellman ford algorithm — Step-1 for Bellman Ford's algorithm

Bellman Ford Pseudocode

We need to maintain the path distance of every vertex. We can store that in an array of size v, where v is the number of vertices.

We also want to be able to get the shortest path, not only know the length of the shortest path. For this, we map each vertex to the vertex that last updated its path length.

Once the algorithm is over, we can backtrack from the destination vertex to the source vertex to find the path.

function bellmanFord(G, S)
for each vertex V in G
distance[V] <- infinite
previous[V] <- NULL
distance[S] <- 0

for each vertex V in G				
for each edge (U,V) in G
tempDistance <- distance[U] + edge_weight(U, V)
if tempDistance < distance[V]
distance[V] <- tempDistance
previous[V] <- U

for each edge (U,V) in G
If distance[U] + edge_weight(U, V) < distance[V}
Error: Negative Cycle Exists

return distance[], previous[]

Bellman Ford vs Dijkstra

Bellman Ford's algorithm and Dijkstra's algorithm are very similar in structure. While Dijkstra looks only to the immediate neighbors of a vertex, Bellman goes through each edge in every iteration.

Dijkstra's vs Bellman Ford's Algorithm — Bellman Ford's Algorithm vs Dijkstra's Algorithm

Python, Java and C/C++ Examples

Python

Java

C++

# Bellman Ford Algorithm in Python


class Graph:

def __init__(self, vertices):
self.V = vertices   # Total number of vertices in the graph
self.graph = []     # Array of edges

# Add edges
def add_edge(self, s, d, w):
self.graph.append([s, d, w])

# Print the solution
def print_solution(self, dist):
print("Vertex Distance from Source")
for i in range(self.V):
print("{0}\t\t{1}".format(i, dist[i]))

def bellman_ford(self, src):

# Step 1: fill the distance array and predecessor array
dist = [float("Inf")] * self.V
# Mark the source vertex
dist[src] = 0

# Step 2: relax edges |V| - 1 times
for _ in range(self.V - 1):
for s, d, w in self.graph:
if dist[s] != float("Inf") and dist[s] + w < dist[d]:
dist[d] = dist[s] + w

# Step 3: detect negative cycle
# if value changes then we have a negative cycle in the graph
# and we cannot find the shortest distances
for s, d, w in self.graph:
if dist[s] != float("Inf") and dist[s] + w < dist[d]:
print("Graph contains negative weight cycle")
return

# No negative weight cycle found!
# Print the distance and predecessor array
self.print_solution(dist)


g = Graph(5)
g.add_edge(0, 1, 5)
g.add_edge(0, 2, 4)
g.add_edge(1, 3, 3)
g.add_edge(2, 1, 6)
g.add_edge(3, 2, 2)

g.bellman_ford(0)

// Bellman Ford Algorithm in Java

class CreateGraph {

// CreateGraph - it consists of edges
class CreateEdge {
int s, d, w;

CreateEdge() {
s = d = w = 0;
}
};

int V, E;
CreateEdge edge[];

// Creates a graph with V vertices and E edges
CreateGraph(int v, int e) {
V = v;
E = e;
edge = new CreateEdge[e];
for (int i = 0; i < e; ++i)
edge[i] = new CreateEdge();
}

void BellmanFord(CreateGraph graph, int s) {
int V = graph.V, E = graph.E;
int dist[] = new int[V];

// Step 1: fill the distance array and predecessor array
for (int i = 0; i < V; ++i)
dist[i] = Integer.MAX_VALUE;

// Mark the source vertex
dist[s] = 0;

// Step 2: relax edges |V| - 1 times
for (int i = 1; i < V; ++i) {
for (int j = 0; j < E; ++j) {
// Get the edge data
int u = graph.edge[j].s;
int v = graph.edge[j].d;
int w = graph.edge[j].w;
if (dist[u] != Integer.MAX_VALUE && dist[u] + w < dist[v])
dist[v] = dist[u] + w;
}
}

// Step 3: detect negative cycle
// if value changes then we have a negative cycle in the graph
// and we cannot find the shortest distances
for (int j = 0; j < E; ++j) {
int u = graph.edge[j].s;
int v = graph.edge[j].d;
int w = graph.edge[j].w;
if (dist[u] != Integer.MAX_VALUE && dist[u] + w < dist[v]) {
System.out.println("CreateGraph contains negative w cycle");
return;
}
}

// No negative w cycle found!
// Print the distance and predecessor array
printSolution(dist, V);
}

// Print the solution
void printSolution(int dist[], int V) {
System.out.println("Vertex Distance from Source");
for (int i = 0; i < V; ++i)
System.out.println(i + "\t\t" + dist[i]);
}

public static void main(String[] args) {
int V = 5; // Total vertices
int E = 8; // Total Edges

CreateGraph graph = new CreateGraph(V, E);

// edge 0 --> 1
graph.edge[0].s = 0;
graph.edge[0].d = 1;
graph.edge[0].w = 5;

// edge 0 --> 2
graph.edge[1].s = 0;
graph.edge[1].d = 2;
graph.edge[1].w = 4;

// edge 1 --> 3
graph.edge[2].s = 1;
graph.edge[2].d = 3;
graph.edge[2].w = 3;

// edge 2 --> 1
graph.edge[3].s = 2;
graph.edge[3].d = 1;
graph.edge[3].w = 6;

// edge 3 --> 2
graph.edge[4].s = 3;
graph.edge[4].d = 2;
graph.edge[4].w = 2;

graph.BellmanFord(graph, 0); // 0 is the source vertex
}
}

// Bellman Ford Algorithm in C

#include <stdio.h>
#include <stdlib.h>

#define INFINITY 99999

//struct for the edges of the graph
struct Edge {
int u;  //start vertex of the edge
int v;  //end vertex of the edge
int w;  //weight of the edge (u,v)
};

//Graph - it consists of edges
struct Graph {
int V;        //total number of vertices in the graph
int E;        //total number of edges in the graph
struct Edge *edge;  //array of edges
};

void bellmanford(struct Graph *g, int source);
void display(int arr[], int size);

int main(void) {
//create graph
struct Graph *g = (struct Graph *)malloc(sizeof(struct Graph));
g->V = 4;  //total vertices
g->E = 5;  //total edges

//array of edges for graph
g->edge = (struct Edge *)malloc(g->E * sizeof(struct Edge));

//------- adding the edges of the graph
/*
edge(u, v)
where 	u = start vertex of the edge (u,v)
          v = end vertex of the edge (u,v)

w is the weight of the edge (u,v)
*/

//edge 0 --> 1
g->edge[0].u = 0;
g->edge[0].v = 1;
g->edge[0].w = 5;

//edge 0 --> 2
g->edge[1].u = 0;
g->edge[1].v = 2;
g->edge[1].w = 4;

//edge 1 --> 3
g->edge[2].u = 1;
g->edge[2].v = 3;
g->edge[2].w = 3;

//edge 2 --> 1
g->edge[3].u = 2;
g->edge[3].v = 1;
g->edge[3].w = 6;

//edge 3 --> 2
g->edge[4].u = 3;
g->edge[4].v = 2;
g->edge[4].w = 2;

bellmanford(g, 0);  //0 is the source vertex

return 0;
}

void bellmanford(struct Graph *g, int source) {
//variables
int i, j, u, v, w;

//total vertex in the graph g
int tV = g->V;

//total edge in the graph g
int tE = g->E;

//distance array
//size equal to the number of vertices of the graph g
int d[tV];

//predecessor array
//size equal to the number of vertices of the graph g
int p[tV];

//step 1: fill the distance array and predecessor array
for (i = 0; i < tV; i++) {
d[i] = INFINITY;
p[i] = 0;
}

//mark the source vertex
d[source] = 0;

//step 2: relax edges |V| - 1 times
for (i = 1; i <= tV - 1; i++) {
for (j = 0; j < tE; j++) {
//get the edge data
u = g->edge[j].u;
v = g->edge[j].v;
w = g->edge[j].w;

if (d[u] != INFINITY && d[v] > d[u] + w) {
d[v] = d[u] + w;
p[v] = u;
}
}
}

//step 3: detect negative cycle
//if value changes then we have a negative cycle in the graph
//and we cannot find the shortest distances
for (i = 0; i < tE; i++) {
u = g->edge[i].u;
v = g->edge[i].v;
w = g->edge[i].w;
if (d[u] != INFINITY && d[v] > d[u] + w) {
printf("Negative weight cycle detected!\n");
return;
}
}

//No negative weight cycle found!
//print the distance and predecessor array
printf("Distance array: ");
display(d, tV);
printf("Predecessor array: ");
display(p, tV);
}

void display(int arr[], int size) {
int i;
for (i = 0; i < size; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}

// Bellman Ford Algorithm in C++

#include <bits/stdc++.h>

// Struct for the edges of the graph
struct Edge {
int u;  //start vertex of the edge
int v;  //end vertex of the edge
int w;  //w of the edge (u,v)
};

// Graph - it consists of edges
struct Graph {
int V;        // Total number of vertices in the graph
int E;        // Total number of edges in the graph
struct Edge* edge;  // Array of edges
};

// Creates a graph with V vertices and E edges
struct Graph* createGraph(int V, int E) {
struct Graph* graph = new Graph;
graph->V = V;  // Total Vertices
graph->E = E;  // Total edges

// Array of edges for graph
graph->edge = new Edge[E];
return graph;
}

// Printing the solution
void printArr(int arr[], int size) {
int i;
for (i = 0; i < size; i++) {
printf("%d ", arr[i]);
}
printf("\n");
}

void BellmanFord(struct Graph* graph, int u) {
int V = graph->V;
int E = graph->E;
int dist[V];

// Step 1: fill the distance array and predecessor array
for (int i = 0; i < V; i++)
dist[i] = INT_MAX;

// Mark the source vertex
dist[u] = 0;

// Step 2: relax edges |V| - 1 times
for (int i = 1; i <= V - 1; i++) {
for (int j = 0; j < E; j++) {
// Get the edge data
int u = graph->edge[j].u;
int v = graph->edge[j].v;
int w = graph->edge[j].w;
if (dist[u] != INT_MAX && dist[u] + w < dist[v])
dist[v] = dist[u] + w;
}
}

// Step 3: detect negative cycle
// if value changes then we have a negative cycle in the graph
// and we cannot find the shortest distances
for (int i = 0; i < E; i++) {
int u = graph->edge[i].u;
int v = graph->edge[i].v;
int w = graph->edge[i].w;
if (dist[u] != INT_MAX && dist[u] + w < dist[v]) {
printf("Graph contains negative w cycle");
return;
}
}

// No negative weight cycle found!
// Print the distance and predecessor array
printArr(dist, V);

return;
}

int main() {
// Create a graph
int V = 5;  // Total vertices
int E = 8;  // Total edges

// Array of edges for graph
struct Graph* graph = createGraph(V, E);

//------- adding the edges of the graph
/*
edge(u, v)
where 	u = start vertex of the edge (u,v)
          v = end vertex of the edge (u,v)

w is the weight of the edge (u,v)
*/

//edge 0 --> 1
graph->edge[0].u = 0;
graph->edge[0].v = 1;
graph->edge[0].w = 5;

//edge 0 --> 2
graph->edge[1].u = 0;
graph->edge[1].v = 2;
graph->edge[1].w = 4;

//edge 1 --> 3
graph->edge[2].u = 1;
graph->edge[2].v = 3;
graph->edge[2].w = 3;

//edge 2 --> 1
graph->edge[3].u = 2;
graph->edge[3].v = 1;
graph->edge[3].w = 6;

//edge 3 --> 2
graph->edge[4].u = 3;
graph->edge[4].v = 2;
graph->edge[4].w = 2;

BellmanFord(graph, 0);  //0 is the source vertex

return 0;
}

Bellman Ford's Complexity

Time Complexity

Best Case Complexity	O(E)
Average Case Complexity	O(VE)
Worst Case Complexity	O(VE)

Space Complexity

And, the space complexity is O(V).

Bellman Ford's Algorithm Applications

For calculating shortest paths in routing algorithms
For finding the shortest path

Page Index

Bellman Ford's Algorithm