Binary search tree is a data structure that quickly allows us to maintain a sorted list of numbers.
- It is called a binary tree because each tree node has a maximum of two children.
- It is called a search tree because it can be used to search for the presence of a number in
O(log(n))time.
The properties that separate a binary search tree from a regular binary tree is
- All nodes of left subtree are less than the root node
- All nodes of right subtree are more than the root node
- Both subtrees of each node are also BSTs i.e. they have the above two properties
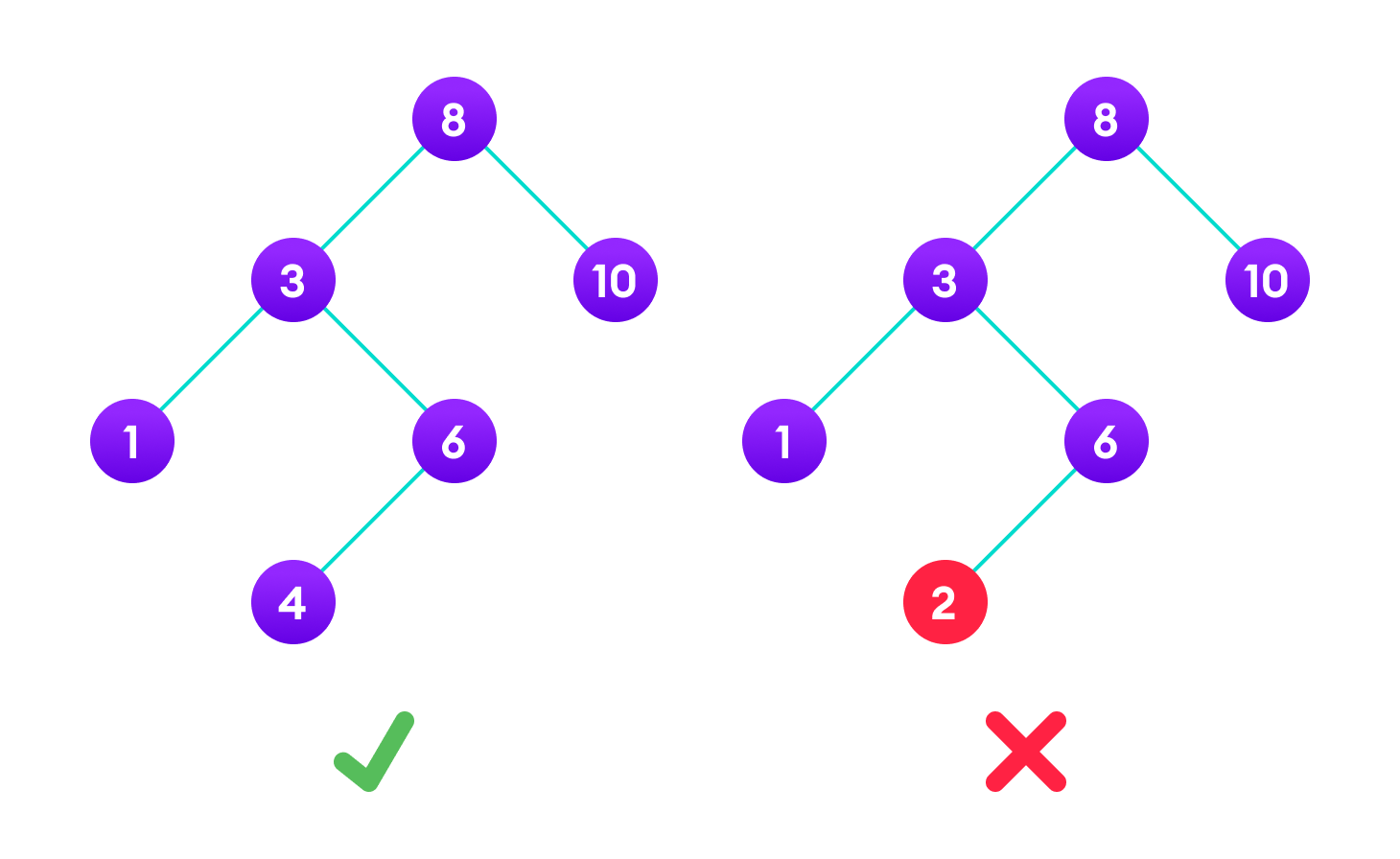
The binary tree on the right isn't a binary search tree because the right subtree of the node "3" contains a value smaller than it.
There are two basic operations that you can perform on a binary search tree:
Search Operation
The algorithm depends on the property of BST that if each left subtree has values below root and each right subtree has values above the root.
If the value is below the root, we can say for sure that the value is not in the right subtree; we need to only search in the left subtree and if the value is above the root, we can say for sure that the value is not in the left subtree; we need to only search in the right subtree.
Algorithm:
If root == NULL
return NULL;
If number == root->data
return root->data;
If number < root->data
return search(root->left)
If number > root->data
return search(root->right)Let us try to visualize this with a diagram.




If the value is found, we return the value so that it gets propagated in each recursion step as shown in the image below.
If you might have noticed, we have called return search(struct node*) four times. When we return either the new node or NULL, the value gets returned again and again until search(root) returns the final result.

If the value is not found, we eventually reach the left or right child of a leaf node which is NULL and it gets propagated and returned.
Insert Operation
Inserting a value in the correct position is similar to searching because we try to maintain the rule that the left subtree is lesser than root and the right subtree is larger than root.
We keep going to either right subtree or left subtree depending on the value and when we reach a point left or right subtree is null, we put the new node there.
Algorithm:
If node == NULL
return createNode(data)
if (data < node->data)
node->left = insert(node->left, data);
else if (data > node->data)
node->right = insert(node->right, data);
return node;The algorithm isn't as simple as it looks. Let's try to visualize how we add a number to an existing BST.




We have attached the node but we still have to exit from the function without doing any damage to the rest of the tree. This is where the return node; at the end comes in handy. In the case of NULL, the newly created node is returned and attached to the parent node, otherwise the same node is returned without any change as we go up until we return to the root.
This makes sure that as we move back up the tree, the other node connections aren't changed.

Deletion Operation
There are three cases for deleting a node from a binary search tree.
Case I
In the first case, the node to be deleted is the leaf node. In such a case, simply delete the node from the tree.


Case II
In the second case, the node to be deleted lies has a single child node. In such a case follow the steps below:
- Replace that node with its child node.
- Remove the child node from its original position.



Case III
In the third case, the node to be deleted has two children. In such a case follow the steps below:
- Get the inorder successor of that node.
- Replace the node with the inorder successor.
- Remove the inorder successor from its original position.



Python, Java and C/C++ Examples
# Binary Search Tree operations in Python
# Create a node
class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
# Inorder traversal
def inorder(root):
if root is not None:
# Traverse left
inorder(root.left)
# Traverse root
print(str(root.key) + "->", end=' ')
# Traverse right
inorder(root.right)
# Insert a node
def insert(node, key):
# Return a new node if the tree is empty
if node is None:
return Node(key)
# Traverse to the right place and insert the node
if key < node.key:
node.left = insert(node.left, key)
else:
node.right = insert(node.right, key)
return node
# Find the inorder successor
def minValueNode(node):
current = node
# Find the leftmost leaf
while(current.left is not None):
current = current.left
return current
# Deleting a node
def deleteNode(root, key):
# Return if the tree is empty
if root is None:
return root
# Find the node to be deleted
if key < root.key:
root.left = deleteNode(root.left, key)
elif(key > root.key):
root.right = deleteNode(root.right, key)
else:
# If the node is with only one child or no child
if root.left is None:
temp = root.right
root = None
return temp
elif root.right is None:
temp = root.left
root = None
return temp
# If the node has two children,
# place the inorder successor in position of the node to be deleted
temp = minValueNode(root.right)
root.key = temp.key
# Delete the inorder successor
root.right = deleteNode(root.right, temp.key)
return root
root = None
root = insert(root, 8)
root = insert(root, 3)
root = insert(root, 1)
root = insert(root, 6)
root = insert(root, 7)
root = insert(root, 10)
root = insert(root, 14)
root = insert(root, 4)
print("Inorder traversal: ", end=' ')
inorder(root)
print("\nDelete 10")
root = deleteNode(root, 10)
print("Inorder traversal: ", end=' ')
inorder(root)// Binary Search Tree operations in Java
class BinarySearchTree {
class Node {
int key;
Node left, right;
public Node(int item) {
key = item;
left = right = null;
}
}
Node root;
BinarySearchTree() {
root = null;
}
void insert(int key) {
root = insertKey(root, key);
}
// Insert key in the tree
Node insertKey(Node root, int key) {
// Return a new node if the tree is empty
if (root == null) {
root = new Node(key);
return root;
}
// Traverse to the right place and insert the node
if (key < root.key)
root.left = insertKey(root.left, key);
else if (key > root.key)
root.right = insertKey(root.right, key);
return root;
}
void inorder() {
inorderRec(root);
}
// Inorder Traversal
void inorderRec(Node root) {
if (root != null) {
inorderRec(root.left);
System.out.print(root.key + " -> ");
inorderRec(root.right);
}
}
void deleteKey(int key) {
root = deleteRec(root, key);
}
Node deleteRec(Node root, int key) {
// Return if the tree is empty
if (root == null)
return root;
// Find the node to be deleted
if (key < root.key)
root.left = deleteRec(root.left, key);
else if (key > root.key)
root.right = deleteRec(root.right, key);
else {
// If the node is with only one child or no child
if (root.left == null)
return root.right;
else if (root.right == null)
return root.left;
// If the node has two children
// Place the inorder successor in position of the node to be deleted
root.key = minValue(root.right);
// Delete the inorder successor
root.right = deleteRec(root.right, root.key);
}
return root;
}
// Find the inorder successor
int minValue(Node root) {
int minv = root.key;
while (root.left != null) {
minv = root.left.key;
root = root.left;
}
return minv;
}
// Driver Program to test above functions
public static void main(String[] args) {
BinarySearchTree tree = new BinarySearchTree();
tree.insert(8);
tree.insert(3);
tree.insert(1);
tree.insert(6);
tree.insert(7);
tree.insert(10);
tree.insert(14);
tree.insert(4);
System.out.print("Inorder traversal: ");
tree.inorder();
System.out.println("\n\nAfter deleting 10");
tree.deleteKey(10);
System.out.print("Inorder traversal: ");
tree.inorder();
}
}// Binary Search Tree operations in C
#include <stdio.h>
#include <stdlib.h>
struct node {
int key;
struct node *left, *right;
};
// Create a node
struct node *newNode(int item) {
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Inorder Traversal
void inorder(struct node *root) {
if (root != NULL) {
// Traverse left
inorder(root->left);
// Traverse root
printf("%d -> ", root->key);
// Traverse right
inorder(root->right);
}
}
// Insert a node
struct node *insert(struct node *node, int key) {
// Return a new node if the tree is empty
if (node == NULL) return newNode(key);
// Traverse to the right place and insert the node
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
// Find the inorder successor
struct node *minValueNode(struct node *node) {
struct node *current = node;
// Find the leftmost leaf
while (current && current->left != NULL)
current = current->left;
return current;
}
// Deleting a node
struct node *deleteNode(struct node *root, int key) {
// Return if the tree is empty
if (root == NULL) return root;
// Find the node to be deleted
if (key < root->key)
root->left = deleteNode(root->left, key);
else if (key > root->key)
root->right = deleteNode(root->right, key);
else {
// If the node is with only one child or no child
if (root->left == NULL) {
struct node *temp = root->right;
free(root);
return temp;
} else if (root->right == NULL) {
struct node *temp = root->left;
free(root);
return temp;
}
// If the node has two children
struct node *temp = minValueNode(root->right);
// Place the inorder successor in position of the node to be deleted
root->key = temp->key;
// Delete the inorder successor
root->right = deleteNode(root->right, temp->key);
}
return root;
}
// Driver code
int main() {
struct node *root = NULL;
root = insert(root, 8);
root = insert(root, 3);
root = insert(root, 1);
root = insert(root, 6);
root = insert(root, 7);
root = insert(root, 10);
root = insert(root, 14);
root = insert(root, 4);
printf("Inorder traversal: ");
inorder(root);
printf("\nAfter deleting 10\n");
root = deleteNode(root, 10);
printf("Inorder traversal: ");
inorder(root);
}// Binary Search Tree operations in C++
#include <iostream>
using namespace std;
struct node {
int key;
struct node *left, *right;
};
// Create a node
struct node *newNode(int item) {
struct node *temp = (struct node *)malloc(sizeof(struct node));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
// Inorder Traversal
void inorder(struct node *root) {
if (root != NULL) {
// Traverse left
inorder(root->left);
// Traverse root
cout << root->key << " -> ";
// Traverse right
inorder(root->right);
}
}
// Insert a node
struct node *insert(struct node *node, int key) {
// Return a new node if the tree is empty
if (node == NULL) return newNode(key);
// Traverse to the right place and insert the node
if (key < node->key)
node->left = insert(node->left, key);
else
node->right = insert(node->right, key);
return node;
}
// Find the inorder successor
struct node *minValueNode(struct node *node) {
struct node *current = node;
// Find the leftmost leaf
while (current && current->left != NULL)
current = current->left;
return current;
}
// Deleting a node
struct node *deleteNode(struct node *root, int key) {
// Return if the tree is empty
if (root == NULL) return root;
// Find the node to be deleted
if (key < root->key)
root->left = deleteNode(root->left, key);
else if (key > root->key)
root->right = deleteNode(root->right, key);
else {
// If the node is with only one child or no child
if (root->left == NULL) {
struct node *temp = root->right;
free(root);
return temp;
} else if (root->right == NULL) {
struct node *temp = root->left;
free(root);
return temp;
}
// If the node has two children
struct node *temp = minValueNode(root->right);
// Place the inorder successor in position of the node to be deleted
root->key = temp->key;
// Delete the inorder successor
root->right = deleteNode(root->right, temp->key);
}
return root;
}
// Driver code
int main() {
struct node *root = NULL;
root = insert(root, 8);
root = insert(root, 3);
root = insert(root, 1);
root = insert(root, 6);
root = insert(root, 7);
root = insert(root, 10);
root = insert(root, 14);
root = insert(root, 4);
cout << "Inorder traversal: ";
inorder(root);
cout << "\nAfter deleting 10\n";
root = deleteNode(root, 10);
cout << "Inorder traversal: ";
inorder(root);
}Binary Search Tree Complexities
Time Complexity
| Operation | Best Case Complexity | Average Case Complexity | Worst Case Complexity |
| Search | O(log n) | O(log n) | O(n) |
| Insertion | O(log n) | O(log n) | O(n) |
| Deletion | O(log n) | O(log n) | O(n) |
Here, n is the number of nodes in the tree.
Space Complexity
The space complexity for all the operations is O(n).
Binary Search Tree Applications
- In multilevel indexing in the database
- For dynamic sorting
- For managing virtual memory areas in Unix kernel
