Fibonacci Heap

A fibonacci heap is a data structure that consists of a collection of trees which follow min heap or max heap property. We have already discussed min heap and max heap property in the Heap Data Structure article. These two properties are the characteristics of the trees present on a fibonacci heap.

In a fibonacci heap, a node can have more than two children or no children at all. Also, it has more efficient heap operations than that supported by the binomial and binary heaps.

The fibonacci heap is called a fibonacci heap because the trees are constructed in a way such that a tree of order n has at least F_n+2 nodes in it, where F_n+2 is the (n + 2)^th Fibonacci number.

Properties of a Fibonacci Heap

Important properties of a Fibonacci heap are:

It is a set of min heap-ordered trees. (i.e. The parent is always smaller than the children.)
A pointer is maintained at the minimum element node.
It consists of a set of marked nodes. (Decrease key operation)
The trees within a Fibonacci heap are unordered but rooted.

Memory Representation of the Nodes in a Fibonacci Heap

The roots of all the trees are linked together for faster access. The child nodes of a parent node are connected to each other through a circular doubly linked list as shown below.

There are two main advantages of using a circular doubly linked list.

Deleting a node from the tree takes O(1) time.
The concatenation of two such lists takes O(1) time.

Operations on a Fibonacci Heap

Insertion

Algorithm

insert(H, x)
degree[x] = 0
p[x] = NIL
child[x] = NIL
left[x] = x
right[x] = x
mark[x] = FALSE
concatenate the root list containing x with root list H 
if min[H] == NIL or key[x] < key[min[H]]
then min[H] = x
n[H] = n[H] + 1

Inserting a node into an already existing heap follows the steps below.

Create a new node for the element.
Check if the heap is empty.
If the heap is empty, set the new node as a root node and mark it min.
Else, insert the node into the root list and update min.

Insertion operation in fibonacci heap — Insertion Example

Find Min

The minimum element is always given by the min pointer.

Union

Union of two fibonacci heaps consists of following steps.

Concatenate the roots of both the heaps.
Update min by selecting a minimum key from the new root lists.

Extract Min

It is the most important operation on a fibonacci heap. In this operation, the node with minimum value is removed from the heap and the tree is re-adjusted.

The following steps are followed:

Delete the min node.
Set the min-pointer to the next root in the root list.
Create an array of size equal to the maximum degree of the trees in the heap before deletion.
Do the following (steps 5-7) until there are no multiple roots with the same degree.
Map the degree of current root (min-pointer) to the degree in the array.
Map the degree of next root to the degree in array.
If there are more than two mappings for the same degree, then apply union operation to those roots such that the min-heap property is maintained (i.e. the minimum is at the root).

An implementation of the above steps can be understood in the example below.

We will perform an extract-min operation on the heap below.
Fibonacci Heap
Delete the min node, add all its child nodes to the root list and set the min-pointer to the next root in the root list.
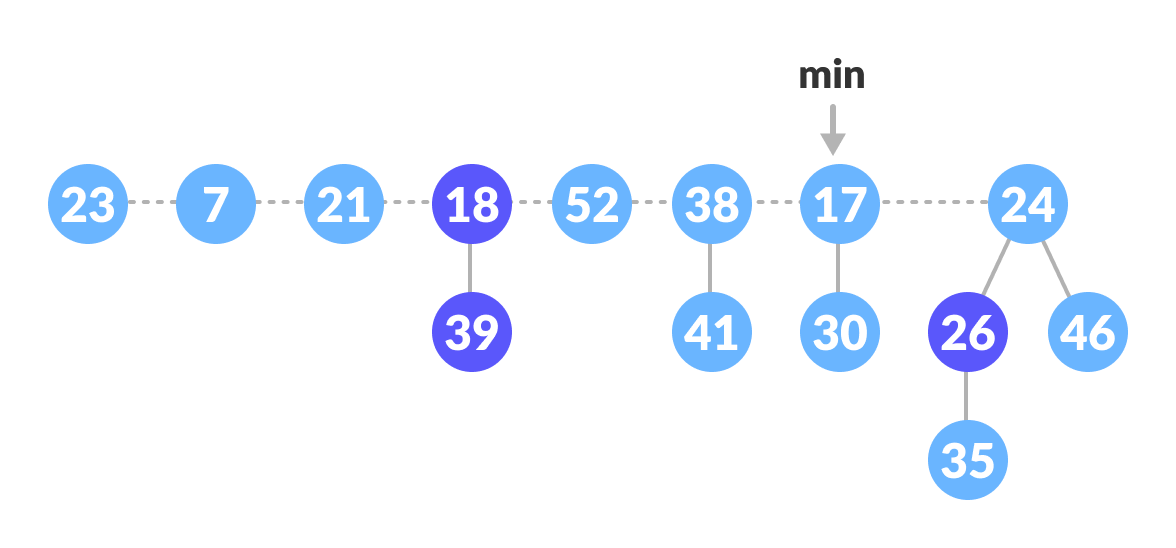
Delete the min node
The maximum degree in the tree is 3. Create an array of size 4 and map degree of the next roots with the array.
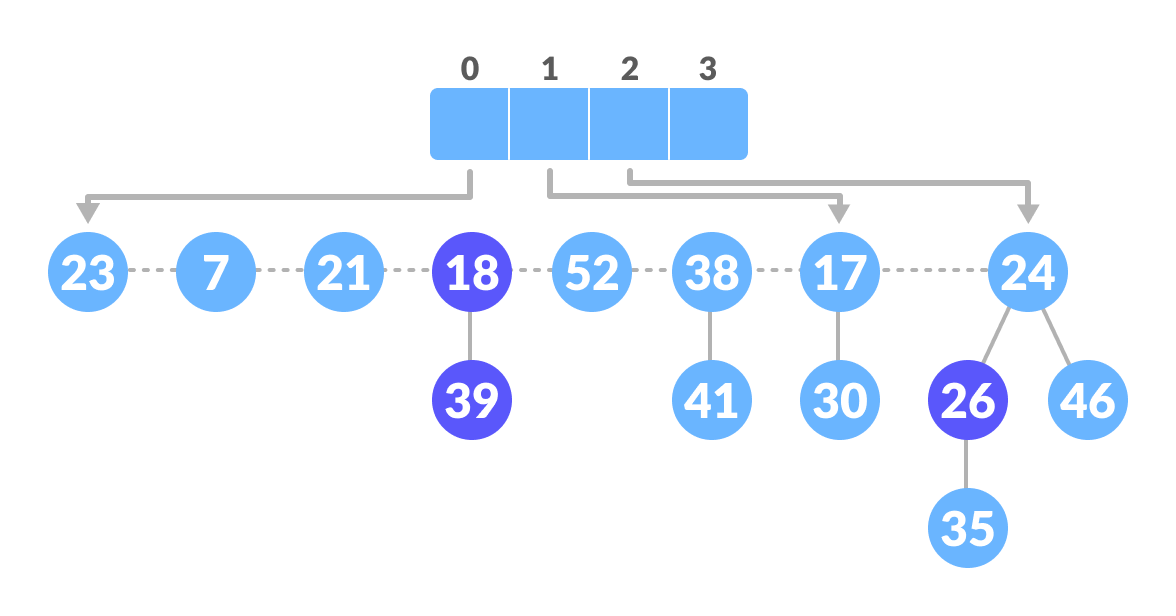
Create an array
Here, 23 and 7 have the same degrees, so unite them.
Unite those having the same degrees
Again, 7 and 17 have the same degrees, so unite them as well.
Unite those having the same degrees
Again 7 and 24 have the same degree, so unite them.
Unite those having the same degrees
Map the next nodes.
Map the remaining nodes
Again, 52 and 21 have the same degree, so unite them
Unite those having the same degrees
Similarly, unite 21 and 18.
Unite those having the same degrees
Map the remaining root.
Map the remaining nodes
The final heap is.
Final fibonacci heap

Decreasing a Key and Deleting a Node

These are the most important operations which are discussed in Decrease Key and Delete Node Operations.

Python, Java and C/C++ Examples

Python

Java

C++

# Fibonacci Heap in python

import math

# Creating fibonacci tree
class FibonacciTree:
def __init__(self, value):
self.value = value
self.child = []
self.order = 0

# Adding tree at the end of the tree
def add_at_end(self, t):
self.child.append(t)
self.order = self.order + 1


# Creating Fibonacci heap
class FibonacciHeap:
def __init__(self):
self.trees = []
self.least = None
self.count = 0

# Insert a node
def insert_node(self, value):
new_tree = FibonacciTree(value)
self.trees.append(new_tree)
if (self.least is None or value < self.least.value):
self.least = new_tree
self.count = self.count + 1

# Get minimum value
def get_min(self):
if self.least is None:
return None
return self.least.value

# Extract the minimum value
def extract_min(self):
smallest = self.least
if smallest is not None:
for child in smallest.child:
self.trees.append(child)
self.trees.remove(smallest)
if self.trees == []:
self.least = None
else:
self.least = self.trees[0]
self.consolidate()
self.count = self.count - 1
return smallest.value

# Consolidate the tree
def consolidate(self):
aux = (floor_log(self.count) + 1) * [None]

while self.trees != []:
x = self.trees[0]
order = x.order
self.trees.remove(x)
while aux[order] is not None:
y = aux[order]
if x.value > y.value:
x, y = y, x
x.add_at_end(y)
aux[order] = None
order = order + 1
aux[order] = x

self.least = None
for k in aux:
if k is not None:
self.trees.append(k)
if (self.least is None
  or k.value < self.least.value):
self.least = k


def floor_log(x):
return math.frexp(x)[1] - 1


fibonacci_heap = FibonacciHeap()

fibonacci_heap.insert_node(7)
fibonacci_heap.insert_node(3)
fibonacci_heap.insert_node(17)
fibonacci_heap.insert_node(24)

print('the minimum value of the fibonacci heap: {}'.format(fibonacci_heap.get_min()))

print('the minimum value removed: {}'.format(fibonacci_heap.extract_min()))

// Operations on Fibonacci Heap in Java

// Node creation
class node {
node parent;
node left;
node right;
node child;
int degree;
boolean mark;
int key;

public node() {
this.degree = 0;
this.mark = false;
this.parent = null;
this.left = this;
this.right = this;
this.child = null;
this.key = Integer.MAX_VALUE;
}

node(int x) {
this();
this.key = x;
}

void set_parent(node x) {
this.parent = x;
}

node get_parent() {
return this.parent;
}

void set_left(node x) {
this.left = x;
}

node get_left() {
return this.left;
}

void set_right(node x) {
this.right = x;
}

node get_right() {
return this.right;
}

void set_child(node x) {
this.child = x;
}

node get_child() {
return this.child;
}

void set_degree(int x) {
this.degree = x;
}

int get_degree() {
return this.degree;
}

void set_mark(boolean m) {
this.mark = m;
}

boolean get_mark() {
return this.mark;
}

void set_key(int x) {
this.key = x;
}

int get_key() {
return this.key;
}
}

public class fibHeap {
node min;
int n;
boolean trace;
node found;

public boolean get_trace() {
return trace;
}

public void set_trace(boolean t) {
this.trace = t;
}

public static fibHeap create_heap() {
return new fibHeap();
}

fibHeap() {
min = null;
n = 0;
trace = false;
}

private void insert(node x) {
if (min == null) {
min = x;
x.set_left(min);
x.set_right(min);
} else {
x.set_right(min);
x.set_left(min.get_left());
min.get_left().set_right(x);
min.set_left(x);
if (x.get_key() < min.get_key())
min = x;
}
n += 1;
}

public void insert(int key) {
insert(new node(key));
}

public void display() {
display(min);
System.out.println();
}

private void display(node c) {
System.out.print("(");
if (c == null) {
System.out.print(")");
return;
} else {
node temp = c;
do {
System.out.print(temp.get_key());
node k = temp.get_child();
display(k);
System.out.print("->");
temp = temp.get_right();
} while (temp != c);
System.out.print(")");
}
}

public static void merge_heap(fibHeap H1, fibHeap H2, fibHeap H3) {
H3.min = H1.min;

if (H1.min != null && H2.min != null) {
node t1 = H1.min.get_left();
node t2 = H2.min.get_left();
H1.min.set_left(t2);
t1.set_right(H2.min);
H2.min.set_left(t1);
t2.set_right(H1.min);
}
if (H1.min == null || (H2.min != null && H2.min.get_key() < H1.min.get_key()))
H3.min = H2.min;
H3.n = H1.n + H2.n;
}

public int find_min() {
return this.min.get_key();
}

private void display_node(node z) {
System.out.println("right: " + ((z.get_right() == null) ? "-1" : z.get_right().get_key()));
System.out.println("left: " + ((z.get_left() == null) ? "-1" : z.get_left().get_key()));
System.out.println("child: " + ((z.get_child() == null) ? "-1" : z.get_child().get_key()));
System.out.println("degree " + z.get_degree());
}

public int extract_min() {
node z = this.min;
if (z != null) {
node c = z.get_child();
node k = c, p;
if (c != null) {
do {
p = c.get_right();
insert(c);
c.set_parent(null);
c = p;
} while (c != null && c != k);
}
z.get_left().set_right(z.get_right());
z.get_right().set_left(z.get_left());
z.set_child(null);
if (z == z.get_right())
this.min = null;
else {
this.min = z.get_right();
this.consolidate();
}
this.n -= 1;
return z.get_key();
}
return Integer.MAX_VALUE;
}

public void consolidate() {
double phi = (1 + Math.sqrt(5)) / 2;
int Dofn = (int) (Math.log(this.n) / Math.log(phi));
node[] A = new node[Dofn + 1];
for (int i = 0; i <= Dofn; ++i)
A[i] = null;
node w = min;
if (w != null) {
node check = min;
do {
node x = w;
int d = x.get_degree();
while (A[d] != null) {
node y = A[d];
if (x.get_key() > y.get_key()) {
node temp = x;
x = y;
y = temp;
w = x;
}
fib_heap_link(y, x);
check = x;
A[d] = null;
d += 1;
}
A[d] = x;
w = w.get_right();
} while (w != null && w != check);
this.min = null;
for (int i = 0; i <= Dofn; ++i) {
if (A[i] != null) {
insert(A[i]);
}
}
}
}

// Linking operation
private void fib_heap_link(node y, node x) {
y.get_left().set_right(y.get_right());
y.get_right().set_left(y.get_left());

node p = x.get_child();
if (p == null) {
y.set_right(y);
y.set_left(y);
} else {
y.set_right(p);
y.set_left(p.get_left());
p.get_left().set_right(y);
p.set_left(y);
}
y.set_parent(x);
x.set_child(y);
x.set_degree(x.get_degree() + 1);
y.set_mark(false);
}

// Search operation
private void find(int key, node c) {
if (found != null || c == null)
return;
else {
node temp = c;
do {
if (key == temp.get_key())
found = temp;
else {
node k = temp.get_child();
find(key, k);
temp = temp.get_right();
}
} while (temp != c && found == null);
}
}

public node find(int k) {
found = null;
find(k, this.min);
return found;
}

public void decrease_key(int key, int nval) {
node x = find(key);
decrease_key(x, nval);
}

// Decrease key operation
private void decrease_key(node x, int k) {
if (k > x.get_key())
return;
x.set_key(k);
node y = x.get_parent();
if (y != null && x.get_key() < y.get_key()) {
cut(x, y);
cascading_cut(y);
}
if (x.get_key() < min.get_key())
min = x;
}

// Cut operation
private void cut(node x, node y) {
x.get_right().set_left(x.get_left());
x.get_left().set_right(x.get_right());

y.set_degree(y.get_degree() - 1);

x.set_right(null);
x.set_left(null);
insert(x);
x.set_parent(null);
x.set_mark(false);
}

private void cascading_cut(node y) {
node z = y.get_parent();
if (z != null) {
if (y.get_mark() == false)
y.set_mark(true);
else {
cut(y, z);
cascading_cut(z);
}
}
}

// Delete operations
public void delete(node x) {
decrease_key(x, Integer.MIN_VALUE);
int p = extract_min();
}

public static void main(String[] args) {
fibHeap obj = create_heap();
obj.insert(7);
obj.insert(26);
obj.insert(30);
obj.insert(39);
obj.insert(10);
obj.display();

System.out.println(obj.extract_min());
obj.display();
System.out.println(obj.extract_min());
obj.display();
System.out.println(obj.extract_min());
obj.display();
System.out.println(obj.extract_min());
obj.display();
System.out.println(obj.extract_min());
obj.display();
}
}

// Operations on a Fibonacci heap in C

#include <math.h>
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>

typedef struct _NODE {
int key;
int degree;
struct _NODE *left_sibling;
struct _NODE *right_sibling;
struct _NODE *parent;
struct _NODE *child;
bool mark;
bool visited;
} NODE;

typedef struct fibanocci_heap {
int n;
NODE *min;
int phi;
int degree;
} FIB_HEAP;

FIB_HEAP *make_fib_heap();
void insertion(FIB_HEAP *H, NODE *new, int val);
NODE *extract_min(FIB_HEAP *H);
void consolidate(FIB_HEAP *H);
void fib_heap_link(FIB_HEAP *H, NODE *y, NODE *x);
NODE *find_min_node(FIB_HEAP *H);
void decrease_key(FIB_HEAP *H, NODE *node, int key);
void cut(FIB_HEAP *H, NODE *node_to_be_decrease, NODE *parent_node);
void cascading_cut(FIB_HEAP *H, NODE *parent_node);
void Delete_Node(FIB_HEAP *H, int dec_key);

FIB_HEAP *make_fib_heap() {
FIB_HEAP *H;
H = (FIB_HEAP *)malloc(sizeof(FIB_HEAP));
H->n = 0;
H->min = NULL;
H->phi = 0;
H->degree = 0;
return H;
}

// Printing the heap
void print_heap(NODE *n) {
NODE *x;
for (x = n;; x = x->right_sibling) {
if (x->child == NULL) {
printf("node with no child (%d) \n", x->key);
} else {
printf("NODE(%d) with child (%d)\n", x->key, x->child->key);
print_heap(x->child);
}
if (x->right_sibling == n) {
break;
}
}
}

// Inserting nodes
void insertion(FIB_HEAP *H, NODE *new, int val) {
new = (NODE *)malloc(sizeof(NODE));
new->key = val;
new->degree = 0;
new->mark = false;
new->parent = NULL;
new->child = NULL;
new->visited = false;
new->left_sibling = new;
new->right_sibling = new;
if (H->min == NULL) {
H->min = new;
} else {
H->min->left_sibling->right_sibling = new;
new->right_sibling = H->min;
new->left_sibling = H->min->left_sibling;
H->min->left_sibling = new;
if (new->key < H->min->key) {
H->min = new;
}
}
(H->n)++;
}

// Find min node
NODE *find_min_node(FIB_HEAP *H) {
if (H == NULL) {
printf(" \n Fibonacci heap not yet created \n");
return NULL;
} else
return H->min;
}

// Union operation
FIB_HEAP *unionHeap(FIB_HEAP *H1, FIB_HEAP *H2) {
FIB_HEAP *Hnew;
Hnew = make_fib_heap();
Hnew->min = H1->min;

NODE *temp1, *temp2;
temp1 = Hnew->min->right_sibling;
temp2 = H2->min->left_sibling;

Hnew->min->right_sibling->left_sibling = H2->min->left_sibling;
Hnew->min->right_sibling = H2->min;
H2->min->left_sibling = Hnew->min;
temp2->right_sibling = temp1;

if ((H1->min == NULL) || (H2->min != NULL && H2->min->key < H1->min->key))
Hnew->min = H2->min;
Hnew->n = H1->n + H2->n;
return Hnew;
}

// Calculate the degree
int cal_degree(int n) {
int count = 0;
while (n > 0) {
n = n / 2;
count++;
}
return count;
}

// Consolidate function
void consolidate(FIB_HEAP *H) {
int degree, i, d;
degree = cal_degree(H->n);
NODE *A[degree], *x, *y, *z;
for (i = 0; i <= degree; i++) {
A[i] = NULL;
}
x = H->min;
do {
d = x->degree;
while (A[d] != NULL) {
y = A[d];
if (x->key > y->key) {
NODE *exchange_help;
exchange_help = x;
x = y;
y = exchange_help;
}
if (y == H->min)
H->min = x;
fib_heap_link(H, y, x);
if (y->right_sibling == x)
H->min = x;
A[d] = NULL;
d++;
}
A[d] = x;
x = x->right_sibling;
} while (x != H->min);

H->min = NULL;
for (i = 0; i < degree; i++) {
if (A[i] != NULL) {
A[i]->left_sibling = A[i];
A[i]->right_sibling = A[i];
if (H->min == NULL) {
H->min = A[i];
} else {
H->min->left_sibling->right_sibling = A[i];
A[i]->right_sibling = H->min;
A[i]->left_sibling = H->min->left_sibling;
H->min->left_sibling = A[i];
if (A[i]->key < H->min->key) {
H->min = A[i];
}
}
if (H->min == NULL) {
H->min = A[i];
} else if (A[i]->key < H->min->key) {
H->min = A[i];
}
}
}
}

// Linking
void fib_heap_link(FIB_HEAP *H, NODE *y, NODE *x) {
y->right_sibling->left_sibling = y->left_sibling;
y->left_sibling->right_sibling = y->right_sibling;

if (x->right_sibling == x)
H->min = x;

y->left_sibling = y;
y->right_sibling = y;
y->parent = x;

if (x->child == NULL) {
x->child = y;
}
y->right_sibling = x->child;
y->left_sibling = x->child->left_sibling;
x->child->left_sibling->right_sibling = y;
x->child->left_sibling = y;
if ((y->key) < (x->child->key))
x->child = y;

(x->degree)++;
}

// Extract min
NODE *extract_min(FIB_HEAP *H) {
if (H->min == NULL)
printf("\n The heap is empty");
else {
NODE *temp = H->min;
NODE *pntr;
pntr = temp;
NODE *x = NULL;
if (temp->child != NULL) {
x = temp->child;
do {
pntr = x->right_sibling;
(H->min->left_sibling)->right_sibling = x;
x->right_sibling = H->min;
x->left_sibling = H->min->left_sibling;
H->min->left_sibling = x;
if (x->key < H->min->key)
H->min = x;
x->parent = NULL;
x = pntr;
} while (pntr != temp->child);
}

(temp->left_sibling)->right_sibling = temp->right_sibling;
(temp->right_sibling)->left_sibling = temp->left_sibling;
H->min = temp->right_sibling;

if (temp == temp->right_sibling && temp->child == NULL)
H->min = NULL;
else {
H->min = temp->right_sibling;
consolidate(H);
}
H->n = H->n - 1;
return temp;
}
return H->min;
}

void cut(FIB_HEAP *H, NODE *node_to_be_decrease, NODE *parent_node) {
NODE *temp_parent_check;

if (node_to_be_decrease == node_to_be_decrease->right_sibling)
parent_node->child = NULL;

node_to_be_decrease->left_sibling->right_sibling = node_to_be_decrease->right_sibling;
node_to_be_decrease->right_sibling->left_sibling = node_to_be_decrease->left_sibling;
if (node_to_be_decrease == parent_node->child)
parent_node->child = node_to_be_decrease->right_sibling;
(parent_node->degree)--;

node_to_be_decrease->left_sibling = node_to_be_decrease;
node_to_be_decrease->right_sibling = node_to_be_decrease;
H->min->left_sibling->right_sibling = node_to_be_decrease;
node_to_be_decrease->right_sibling = H->min;
node_to_be_decrease->left_sibling = H->min->left_sibling;
H->min->left_sibling = node_to_be_decrease;

node_to_be_decrease->parent = NULL;
node_to_be_decrease->mark = false;
}

void cascading_cut(FIB_HEAP *H, NODE *parent_node) {
NODE *aux;
aux = parent_node->parent;
if (aux != NULL) {
if (parent_node->mark == false) {
parent_node->mark = true;
} else {
cut(H, parent_node, aux);
cascading_cut(H, aux);
}
}
}

void decrease_key(FIB_HEAP *H, NODE *node_to_be_decrease, int new_key) {
NODE *parent_node;
if (H == NULL) {
printf("\n FIbonacci heap not created ");
return;
}
if (node_to_be_decrease == NULL) {
printf("Node is not in the heap");
}

else {
if (node_to_be_decrease->key < new_key) {
printf("\n Invalid new key for decrease key operation \n ");
} else {
node_to_be_decrease->key = new_key;
parent_node = node_to_be_decrease->parent;
if ((parent_node != NULL) && (node_to_be_decrease->key < parent_node->key)) {
printf("\n cut called");
cut(H, node_to_be_decrease, parent_node);
printf("\n cascading cut called");
cascading_cut(H, parent_node);
}
if (node_to_be_decrease->key < H->min->key) {
H->min = node_to_be_decrease;
}
}
}
}

void *find_node(FIB_HEAP *H, NODE *n, int key, int new_key) {
NODE *find_use = n;
NODE *f = NULL;
find_use->visited = true;
if (find_use->key == key) {
find_use->visited = false;
f = find_use;
decrease_key(H, f, new_key);
}
if (find_use->child != NULL) {
find_node(H, find_use->child, key, new_key);
}
if ((find_use->right_sibling->visited != true)) {
find_node(H, find_use->right_sibling, key, new_key);
}

find_use->visited = false;
}

FIB_HEAP *insertion_procedure() {
FIB_HEAP *temp;
int no_of_nodes, ele, i;
NODE *new_node;
temp = (FIB_HEAP *)malloc(sizeof(FIB_HEAP));
temp = NULL;
if (temp == NULL) {
temp = make_fib_heap();
}
printf(" \n enter number of nodes to be insert = ");
scanf("%d", &no_of_nodes);
for (i = 1; i <= no_of_nodes; i++) {
printf("\n node %d and its key value = ", i);
scanf("%d", &ele);
insertion(temp, new_node, ele);
}
return temp;
}
void Delete_Node(FIB_HEAP *H, int dec_key) {
NODE *p = NULL;
find_node(H, H->min, dec_key, -5000);
p = extract_min(H);
if (p != NULL)
printf("\n Node deleted");
else
printf("\n Node not deleted:some error");
}

int main(int argc, char **argv) {
NODE *new_node, *min_node, *extracted_min, *node_to_be_decrease, *find_use;
FIB_HEAP *heap, *h1, *h2;
int operation_no, new_key, dec_key, ele, i, no_of_nodes;
heap = (FIB_HEAP *)malloc(sizeof(FIB_HEAP));
heap = NULL;
while (1) {
printf(" \n Operations \n 1. Create Fibonacci heap \n 2. Insert nodes into fibonacci heap \n 3. Find min \n 4. Union \n 5. Extract min \n 6. Decrease key \n 7.Delete node \n 8. print heap \n 9. exit \n enter operation_no = ");
scanf("%d", &operation_no);

switch (operation_no) {
case 1:
heap = make_fib_heap();
break;

case 2:
if (heap == NULL) {
heap = make_fib_heap();
}
printf(" enter number of nodes to be insert = ");
scanf("%d", &no_of_nodes);
for (i = 1; i <= no_of_nodes; i++) {
printf("\n node %d and its key value = ", i);
scanf("%d", &ele);
insertion(heap, new_node, ele);
}
break;

case 3:
min_node = find_min_node(heap);
if (min_node == NULL)
printf("No minimum value");
else
printf("\n min value = %d", min_node->key);
break;

case 4:
if (heap == NULL) {
printf("\n no FIbonacci heap created \n ");
break;
}
h1 = insertion_procedure();
heap = unionHeap(heap, h1);
printf("Unified Heap:\n");
print_heap(heap->min);
break;

case 5:
if (heap == NULL)
printf("Empty Fibonacci heap");
else {
extracted_min = extract_min(heap);
printf("\n min value = %d", extracted_min->key);
printf("\n Updated heap: \n");
print_heap(heap->min);
}
break;

case 6:
if (heap == NULL)
printf("Fibonacci heap is empty");
else {
printf(" \n node to be decreased = ");
scanf("%d", &dec_key);
printf(" \n enter the new key = ");
scanf("%d", &new_key);
find_use = heap->min;
find_node(heap, find_use, dec_key, new_key);
printf("\n Key decreased- Corresponding heap:\n");
print_heap(heap->min);
}
break;
case 7:
if (heap == NULL)
printf("Fibonacci heap is empty");
else {
printf(" \n Enter node key to be deleted = ");
scanf("%d", &dec_key);
Delete_Node(heap, dec_key);
printf("\n Node Deleted- Corresponding heap:\n");
print_heap(heap->min);
break;
}
case 8:
print_heap(heap->min);
break;

case 9:
free(new_node);
free(heap);
exit(0);

default:
printf("Invalid choice ");
}
}
}

// Operations on a Fibonacci heap in C++

#include <cmath>
#include <cstdlib>
#include <iostream>

using namespace std;

// Node creation
struct node {
int n;
int degree;
node *parent;
node *child;
node *left;
node *right;
char mark;

char C;
};

// Implementation of Fibonacci heap
class FibonacciHeap {
private:
int nH;

node *H;

public:
node *InitializeHeap();
int Fibonnaci_link(node *, node *, node *);
node *Create_node(int);
node *Insert(node *, node *);
node *Union(node *, node *);
node *Extract_Min(node *);
int Consolidate(node *);
int Display(node *);
node *Find(node *, int);
int Decrease_key(node *, int, int);
int Delete_key(node *, int);
int Cut(node *, node *, node *);
int Cascase_cut(node *, node *);
FibonacciHeap() { H = InitializeHeap(); }
};

// Initialize heap
node *FibonacciHeap::InitializeHeap() {
node *np;
np = NULL;
return np;
}

// Create node
node *FibonacciHeap::Create_node(int value) {
node *x = new node;
x->n = value;
return x;
}

// Insert node
node *FibonacciHeap::Insert(node *H, node *x) {
x->degree = 0;
x->parent = NULL;
x->child = NULL;
x->left = x;
x->right = x;
x->mark = 'F';
x->C = 'N';
if (H != NULL) {
(H->left)->right = x;
x->right = H;
x->left = H->left;
H->left = x;
if (x->n < H->n)
H = x;
} else {
H = x;
}
nH = nH + 1;
return H;
}

// Create linking
int FibonacciHeap::Fibonnaci_link(node *H1, node *y, node *z) {
(y->left)->right = y->right;
(y->right)->left = y->left;
if (z->right == z)
H1 = z;
y->left = y;
y->right = y;
y->parent = z;

if (z->child == NULL)
z->child = y;

y->right = z->child;
y->left = (z->child)->left;
((z->child)->left)->right = y;
(z->child)->left = y;

if (y->n < (z->child)->n)
z->child = y;
z->degree++;
}

// Union Operation
node *FibonacciHeap::Union(node *H1, node *H2) {
node *np;
node *H = InitializeHeap();
H = H1;
(H->left)->right = H2;
(H2->left)->right = H;
np = H->left;
H->left = H2->left;
H2->left = np;
return H;
}

// Display the heap
int FibonacciHeap::Display(node *H) {
node *p = H;
if (p == NULL) {
cout << "Empty Heap" << endl;
return 0;
}
cout << "Root Nodes: " << endl;

do {
cout << p->n;
p = p->right;
if (p != H) {
cout << "-->";
}
} while (p != H && p->right != NULL);
cout << endl;
}

// Extract min
node *FibonacciHeap::Extract_Min(node *H1) {
node *p;
node *ptr;
node *z = H1;
p = z;
ptr = z;
if (z == NULL)
return z;

node *x;
node *np;

x = NULL;

if (z->child != NULL)
x = z->child;

if (x != NULL) {
ptr = x;
do {
np = x->right;
(H1->left)->right = x;
x->right = H1;
x->left = H1->left;
H1->left = x;
if (x->n < H1->n)
H1 = x;

x->parent = NULL;
x = np;
} while (np != ptr);
}

(z->left)->right = z->right;
(z->right)->left = z->left;
H1 = z->right;

if (z == z->right && z->child == NULL)
H = NULL;

else {
H1 = z->right;
Consolidate(H1);
}
nH = nH - 1;
return p;
}

// Consolidation Function
int FibonacciHeap::Consolidate(node *H1) {
int d, i;
float f = (log(nH)) / (log(2));
int D = f;
node *A[D];

for (i = 0; i <= D; i++)
A[i] = NULL;

node *x = H1;
node *y;
node *np;
node *pt = x;

do {
pt = pt->right;

d = x->degree;

while (A[d] != NULL)

{
y = A[d];

if (x->n > y->n)

{
np = x;

x = y;

y = np;
}

if (y == H1)
H1 = x;
Fibonnaci_link(H1, y, x);
if (x->right == x)
H1 = x;
A[d] = NULL;
d = d + 1;
}

A[d] = x;
x = x->right;

}

while (x != H1);
H = NULL;
for (int j = 0; j <= D; j++) {
if (A[j] != NULL) {
A[j]->left = A[j];
A[j]->right = A[j];
if (H != NULL) {
(H->left)->right = A[j];
A[j]->right = H;
A[j]->left = H->left;
H->left = A[j];
if (A[j]->n < H->n)
H = A[j];
} else {
H = A[j];
}
if (H == NULL)
H = A[j];
else if (A[j]->n < H->n)
H = A[j];
}
}
}

// Decrease Key Operation
int FibonacciHeap::Decrease_key(node *H1, int x, int k) {
node *y;
if (H1 == NULL) {
cout << "The Heap is Empty" << endl;
return 0;
}
node *ptr = Find(H1, x);
if (ptr == NULL) {
cout << "Node not found in the Heap" << endl;
return 1;
}

if (ptr->n < k) {
cout << "Entered key greater than current key" << endl;
return 0;
}
ptr->n = k;
y = ptr->parent;
if (y != NULL && ptr->n < y->n) {
Cut(H1, ptr, y);
Cascase_cut(H1, y);
}

if (ptr->n < H->n)
H = ptr;

return 0;
}

// Cutting Function
int FibonacciHeap::Cut(node *H1, node *x, node *y)

{
if (x == x->right)
y->child = NULL;
(x->left)->right = x->right;
(x->right)->left = x->left;
if (x == y->child)
y->child = x->right;
y->degree = y->degree - 1;
x->right = x;
x->left = x;
(H1->left)->right = x;
x->right = H1;
x->left = H1->left;
H1->left = x;
x->parent = NULL;
x->mark = 'F';
}

// Cascade cut
int FibonacciHeap::Cascase_cut(node *H1, node *y) {
node *z = y->parent;
if (z != NULL) {
if (y->mark == 'F') {
y->mark = 'T';
} else

{
Cut(H1, y, z);
Cascase_cut(H1, z);
}
}
}

// Search function
node *FibonacciHeap::Find(node *H, int k) {
node *x = H;
x->C = 'Y';
node *p = NULL;
if (x->n == k) {
p = x;
x->C = 'N';
return p;
}

if (p == NULL) {
if (x->child != NULL)
p = Find(x->child, k);
if ((x->right)->C != 'Y')
p = Find(x->right, k);
}

x->C = 'N';
return p;
}

// Deleting key
int FibonacciHeap::Delete_key(node *H1, int k) {
node *np = NULL;
int t;
t = Decrease_key(H1, k, -5000);
if (!t)
np = Extract_Min(H);
if (np != NULL)
cout << "Key Deleted" << endl;
else
cout << "Key not Deleted" << endl;
return 0;
}

int main() {
int n, m, l;
FibonacciHeap fh;
node *p;
node *H;
H = fh.InitializeHeap();

p = fh.Create_node(7);
H = fh.Insert(H, p);
p = fh.Create_node(3);
H = fh.Insert(H, p);
p = fh.Create_node(17);
H = fh.Insert(H, p);
p = fh.Create_node(24);
H = fh.Insert(H, p);

fh.Display(H);

p = fh.Extract_Min(H);
if (p != NULL)
cout << "The node with minimum key: " << p->n << endl;
else
cout << "Heap is empty" << endl;

m = 26;
l = 16;
fh.Decrease_key(H, m, l);

m = 16;
fh.Delete_key(H, m);
}

Complexities

Insertion	O(1)
Find Min	O(1)
Union	O(1)
Extract Min	O(log n)
Decrease Key	O(1)
Delete Node	O(log n)

Fibonacci Heap Applications

To improve the asymptotic running time of Dijkstra's algorithm.

Page Index